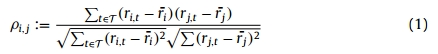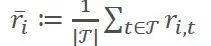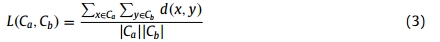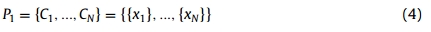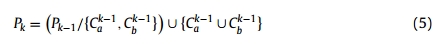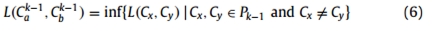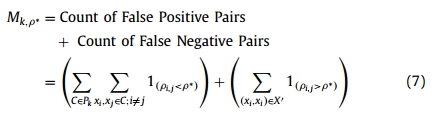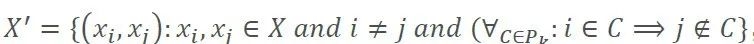摘要
文献来源:Paul Geertsema, Helen Lu, The correlation structure of anomaly strategies, Journal of Banking and Finance, 2020, vol. 119.
推荐原因:本文从大量异象中筛选出显著的异象,并对其进行聚类,合并为28个异象聚类组合。在五因子模型(How等,2020)下,仍然有三分之一的聚类组合收益显著。通过最佳优先搜索算法,从现有因子与聚类组合中寻找到9个因子,能够解释全部的聚类组合以及显著的异象。其中,预期增长因子(EG)和与应计项目相关的聚类组合是提高定价能力的重要因素。
1、简介
许多研究通过提出新的资产定价模型来解释逐渐增多的异象。实际上,这些新提出的风险因子最初就以异象的形式表现。例如,Fama & French(1993)三因子模型中的SMB因子,便是基于Banz(1981)中记录的规模异象。本文利用学术界所发现的大量异象,提出了一种基于异象之间的相关性将异象聚类的新方法,来识别实际收益中没有被当前资产定价模型所包含的维度。
本文从现有文献中构建了包含215种异象策略的数据库。我们的异象策略是用美股构建的多空组合,以分位数分组并以市值加权构建组合。根据Hou等(2015),我们使用5%显著性水平来挑选异象进行进一步研究。通过这种方法,可以得到80个在均值上显著的异象。我们使用聚类分析将这些筛选后的异象划分为28个等权的聚类组合。
我们使用基于相关性的相异性指标,运用层次聚类(hierarchical agglomerative clustering)的聚类方法。在本文中,我们希望将显著相关的异象划分为同一类,其中相关性超过0.4定义为显著相关。我们发现28个集合能够在给定阈值下将异象的错分类水平降至最低,聚类组合的平均相关性为0.03而组间相关性最高为0.57。
聚类组合可以用以识别当前基准模型中遗漏的维度,从而构建更加准确、精确的业绩评价基准。即使使用最严格的模型——五因子模型(Hou等,2020)仍然能够发现28个聚类组合中有10个在5%水平下显著。由于当前的基准模型不能解释这些聚类组合,我们从41个待选因子中寻找其他因子以解释收益。通过最佳优先搜索(Best-First Search)算法,我们发现了9个因子,能够解释所有28个聚类组合及80个显著的异象。这9个因子分别为预期成长(expected growth)因子(Hou等,2020),应计聚类组合(Accruals,如Sloan,1996),SMB市值因子(Fama & French,1993),发行与收益率溢价聚类组合(如Basu,1977,Danial&Titman,2006),市场因子,短期反转因子,季节效应聚类组合,资本增长(CapexGrowth)聚类组合(如Xin,2008),EPS持续性(epsconsistency)聚类组合(长期盈利增长异象,Alwathainani, 2009))。
2. 数据
本文使用了在NYSE, Amex 或者 Nasdaq交易的普通股构建异象策略,得到每月收益。样本期从1963年7月开始,到2019年12月结束。
异象生成方面,作者使用分位数分组并以市值加权构建组合,生成月收益。215个预测排序变量主要分为企业特征、股票变量或者宏观经济因子载荷。
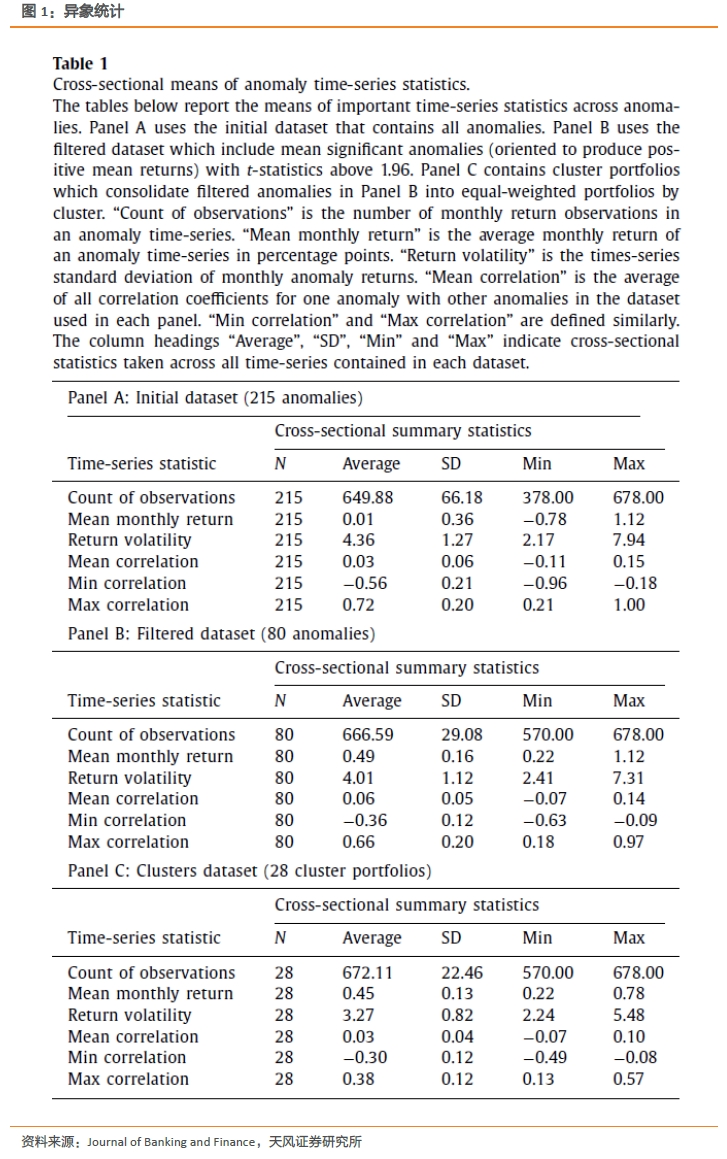
下图表A展示了215种策略的概要信息,表B给出了过滤后的80个异象数据的汇总统计数据,表C中的集群投资组合则是通过计算同一集群中的等权平均收益来构建。如预期的那样,经过过滤的异象非常显著,平均月度收益的均值为0.49%。相关性方面,平均而言,异象之间只有弱正相关。但大多数异象与至少一种异象具有强相关关系。为了处理强相关异象,我们可以将它们分组在同一个聚类组合中。
3. 聚类分析
聚类分析是无监督机器学习的一个分支,用于根据某种相似性概念将实体划分为不同的组。本文使用了聚类分析中的层次聚类。在开始时,每个异象被分配到它自己的集群。在这一点上,有多少异象就有多少集群——在过滤异象的情况下有80个。然后,在每次迭代时,根据指定的条件将两个差异最小的聚类合并到一个新的聚类中。每次迭代都减少一个簇的数量,这样在聚类过程结束时,所有异象都被分配到同一个簇中。
我们选择了N=80个异象,异象集合为,相应的收益率序列为。则异象
和之间相关性可定义为:
其中,|T|表示集合T中元素的个数,
随后,将相关性转化为相异性度量,定义为:
其中,的范围为[0,1],d=0对应完全正相关(ρ=1),d=1对应完全负相关(ρ=-1)。通过指定异象间的相异性,可以将强相关异象聚在一组,而将弱相关异象划分在不同的组。
我们使用平均关联方法(average linkage method)衡量两个类别之间的关系。将X的两个不重叠子集和
(,⊂ X,∩=∅)之间的平均联系L(·)定义为
注意,在特殊情况下=和=平均连杆等于迭代k = 1时,初始集群划分包括N个集群,记为,每个集群包含一个(唯一的)元素。有:
迭代k > 1处的P_k被递归定义为
其中和这两个簇是中满足要求的最不相似的集群,而
因此,在每一次迭代中,两个最不相似的集群和在前一个集群分区中被识别出来。通过删除和,加上由和并集形成的新集群,形成新的集群分区。这些集群都是在X的元素的基础上形成的集合,每个X的元素都出现在给定集群分区中的一个且仅一个集群中。集群分区的序列
被称为集群结构。上述描述也可以表示为一种算法;具体细节如图2所示:
生成集群组合需要确定适当的集群数量。为了让组合能够实现某种程度的独立性,集群的最佳数量应该能最大限度地减少对异象的误分类。考虑到一些因子具有中度甚至实质性的相关性,文章取相关性阈值为0.4。在发生误分类时,如果成对相关性低于阈值却将一对不同的异象分配给同一聚类,称为假阳性;而若成对相关性高于阈值却将一对不同的异象分配给不同的聚类,则称为假阴性。因此,将X上的实体在给定相关性阈值上的对群集P_k的误分类计数定义为:
上式中,
,是分区
中所有不在同一簇内的异象对的集合。条件x为真时,指示函数
,否则为0。
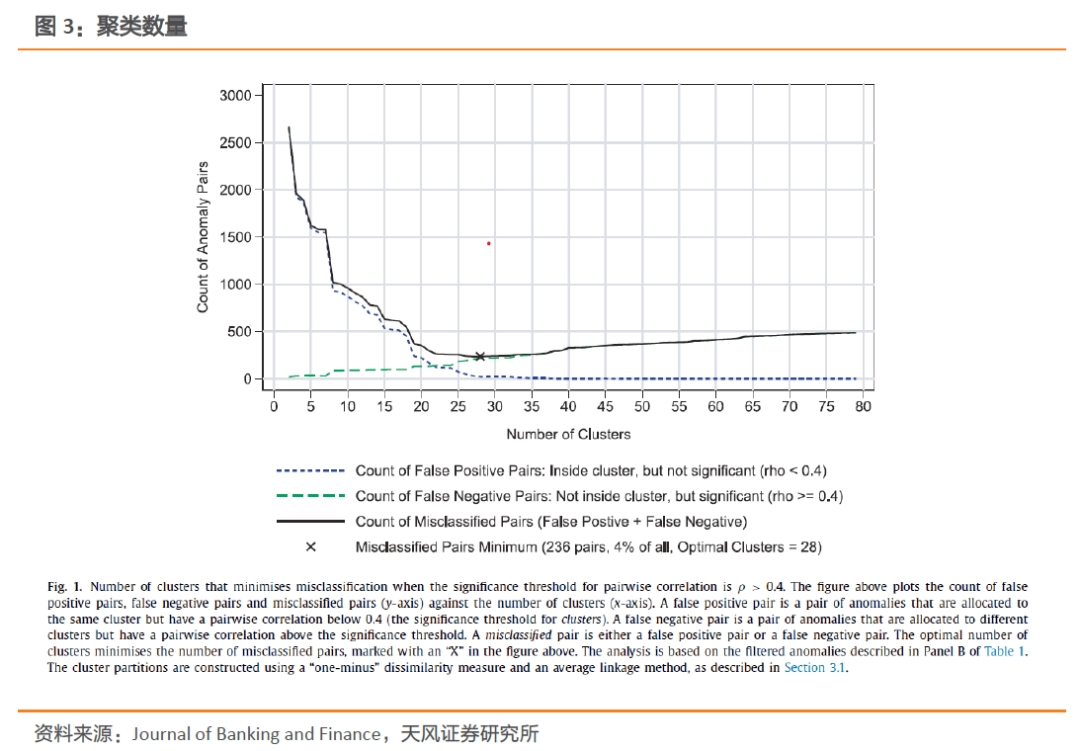
下图绘制了假阳性数、假阴性数和误分类总数相对于聚类数在相关阈值为0.4时的图。结果表明,集群组合个数为28时,在3160对相关中,错误分类的计数最小,为236。
4. 收益的维度
4.1. 聚类组合的alpha与无法解释的方差
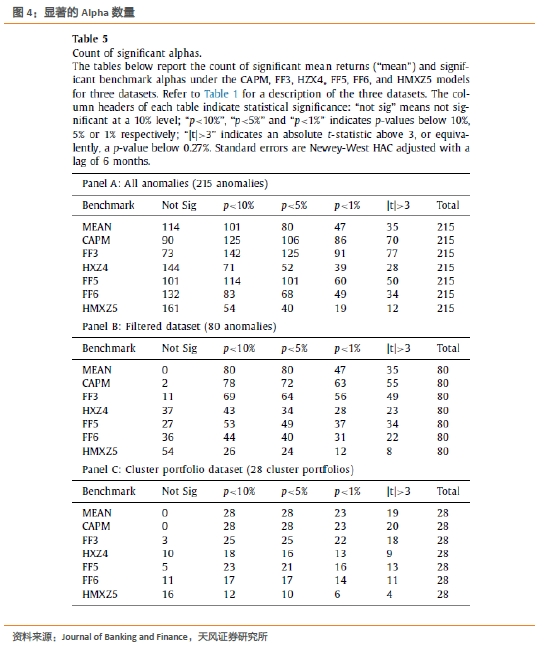
在本节中,本文进行了标准时间序列的alpha检验,以衡量当前的基准模型是否可以解释异象和聚类组合。下图列出了六种不同基准模型和测试中使用的三个数据集,在显著性水平不断增加时,具有显著alpha的异象或集群组合的个数。其中,表A选择所有异象作为测试样本,表B与C的测试样本分别为80个过滤异象和28个集群组合。
测试结果表明,对于不同的样本,HXZ4和HMXZ5模型的表现均为最佳,它们是消除显著alpha的两个最佳模型。此外,在表C的检验中,即使是表现最好的HMXZ5模型,在显著性水平5%情况下,也有10个(36%)集群组合结果显著,这意味着可以向当前的基准模型添加更多维度。
在给定的显著性阈值下,集群的显著性alpha值的百分比要高于异象策略。这表明,当异象本身强相关时,所解释异象的比列可能会夸大基准模型的能力。从这个意义上说,集群投资组合可能提供了一个更均衡的基准。
4.2. 降维搜索
我们识别了备选因子中能够最好地解释所有28个集群投资组合的子集。候选因子一共41个,包括28个聚类组合本身加上13个共同因子(MKTRF、SMB、HML、RMW、CMA、UMD、ROE、EG、LTREV、STREV、QMJ、BAB和HMLdevil)。本文考虑两个目标:第一个目标是减少alpha显著的集群投资组合数量,而第二个目标是减少集群投资组合平均的无法解释的方差。
本文选择了一种贪婪(最佳优先)搜索算法,该策略在每个步骤中都选择能最大限度地减少目标的额外因子。其中,目标可设为显著集群投资组合的数量或平均无法解释的方差,具体视情况而定。在模型中添加额外的因子总是会减少无法解释的方差,直至最后为零。然而,通常情况下,不能通过向当前模型中添加额外的因子来进一步减少显著的集群投资组合的数量。当发生这种情况时,切换到第二阶段搜索策略,该策略将最强的集群投资组合添加到模型中(以alpha的t统计量衡量)。
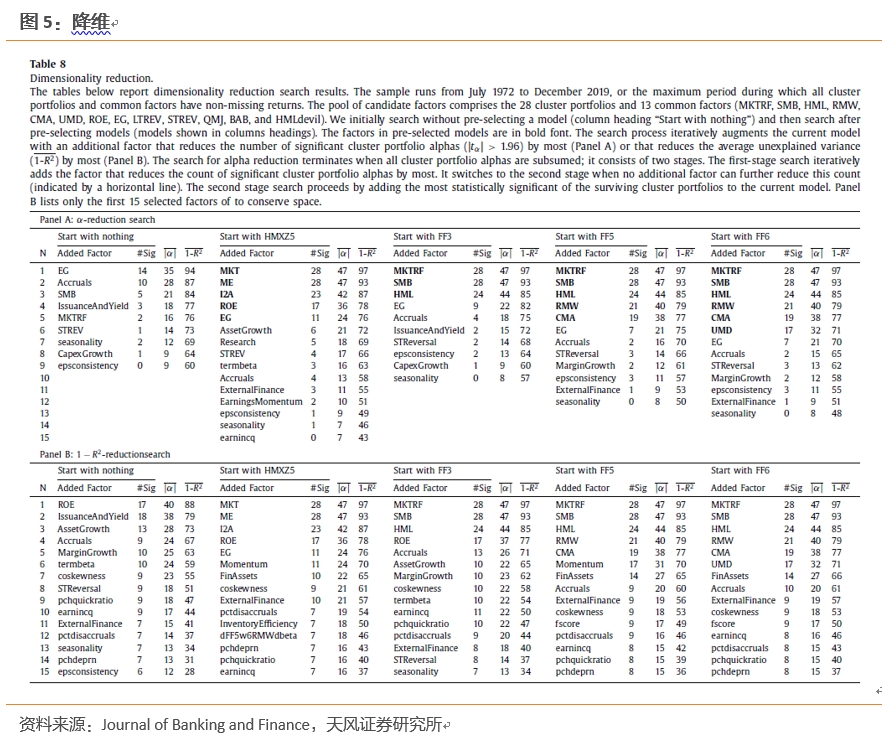
最终,减少alpha的工作确定了组成模型的9个因子,它们可以解释28个集群组合。这些因子包括4个共同因子和5个集群组合;按顺序排列,它们分别是,1)HMXZ5模型的EG(预期增长)因子,2)Accruals集群投资组合,3)FF3模型中的SMB规模因子,4)IssuanceAndYield集群投资组合,5)MKTRF(市场超额收益因子),6)STREV(短期反转因子),7)seasonality集群投资组合,8)CapexGrowth集群投资组合和9)epsconsistency集群投资组合。我们验证了,选择的9个因子可以将筛选的80个异象减少到了不重要的程度,这表明本文所阐述的28个聚类组合是对80个筛选的原始异象的更简介的表达。
需要强调的是,还有其他候选因子集合也能够解释所有的集群组合,我们的搜索结果只证明了上界的存在,可能还存在更简单的模型。
文章还考虑了从预先选定的基准模型的因子开始进行降维搜索。这种分析能够突出在描述异象回报横截面方面能够提供增量的集群投资组合。其中,EG因子和Accruals集群投资组合影响力最大,它们在一起解释了28个集群投资组合中的18个(未报告的结果)——比任何一个基准模型都多。在所有情况下,STREV因子或STReversal集群组合(包含STREV因子)也会被选择。最后,季节性和epsconsistency集群组合也经常选入。这些集群投资组合是高度独立的,将其包含到模型中似乎是解释其的唯一方法。
此外,本文还考虑第二个目标,即哪些因子最适合减少无法解释的方差。减少方差的搜索和减少alpha的搜索会生成稍微不同的因子排名,结果如下图中的表B所示。通过减少方差搜索选择的前九个因子是来自HXZ4模型的ROE(获利能力)因子,其次是IssuanceAndYield,AssetGrowth,Accruals,MarginGrowth,termbeta,coskewness, STReversal和pchquickratio集群投资组合。
总而言之,一个相对简洁的九因子模型包含了全部28个集群组合以及所有80个显著的异象。当增加因子扩充当前的基准模型时,几乎总是首先选择EG(预期增长)因子和Accruals集群投资组合。
5. 资产定价
在基准模型种增加新的因子可以显著提高模型的定价能力。与以减少方差的搜索相比,以减少alpha为目的的搜索更加有效。
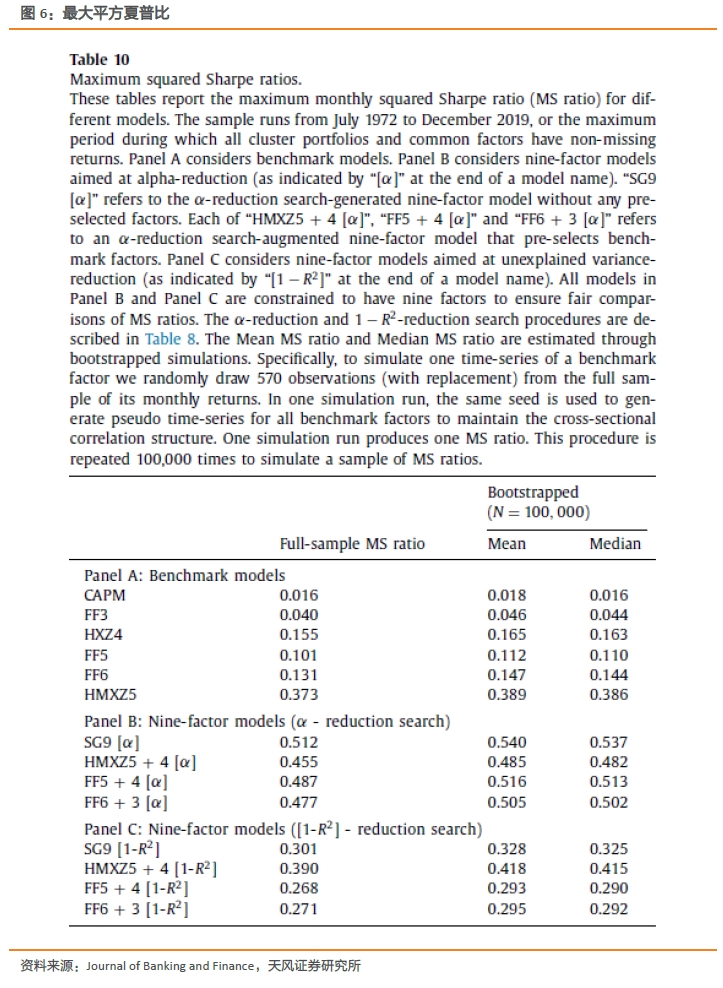
参照Barillas和Shanken(2017)的研究,我们使用基准因子的月度最大夏普比平方(MS比率)来比较基准模型的定价能力。下图结果显示,在全样本中,基准模型里HMXZ5模型的MS比最高,为0.37。而搜索增强模型(SG9)为0.51,远远强于HMXZ5。在利用数据重抽样法进行100,000模拟后,上述结论依旧不变。
6. 总结
本文从215个异象策略中筛选出了80个显著异象,并利用聚类分析将它们合并为28个集群投资组合。在当前的基准模型中,即使是表现最佳的HXMZ5模型仍然使28个集群组合中的10个具有显著性。集群投资组合体现了当前基准模型没有考虑到的预期回报的维度。
本文从41个候选因子中寻找可以解释28个集群组合和80个异象的因子。以降低alpha显著性为目标,最佳优先搜索策略找到9个因子。分别是1)EG(预期增长因子),2)Accruals集群投资组合,3)SMB规模因子,4)IssuanceAndYield集群投资组合,5)MKTRF(市场超额收益因子),6)STREV(短期反转因子),7)seasonality集群投资组合,8)CapexGrowth集群投资组合和9)epsconsistency集群投资组合。
风险提示:本报告内容基于相关文献,不构成投资建议。
注:文中报告节选自天风证券研究所已公开发布研究报告,具体报告内容及相关风险提示等详见完整版报告。
证券研究报告
《天风证券-金融工程:海外文献推荐第154期》
对外发布时间
2020年10月21日(注:报告审核流程结束时间)
报告发布机构
天风证券股份有限公司
(已获中国证监会许可的证券投资咨询业务资格)
本报告分析师
吴先兴 SAC 执业证书编号:S1110516120001
(作者:量化先行者 )
声明:本文由21财经客户端“南财号”平台入驻机构(自媒体)发布,不代表21财经客户端的观点和立场。